Latihan Soal USP - MATEMATIKA IPA
4 Alasan Pentingnya Latihan Soal dalam Hadapi Ujian
1. Terbiasa suasana ujian2. Memahami pola pertanyaan diujikan
3. Mengetahui sejauh mana pemahaman materi
4. Melatih manajemen waktu

LATIHAN USP - MATEMATIKA WAJIB IPS
4 Alasan Pentingnya Latihan Soal dalam Hadapi Ujian
1. Terbiasa suasana ujian2. Memahami pola pertanyaan diujikan
3. Mengetahui sejauh mana pemahaman materi
4. Melatih manajemen waktu

POLINOMIAL
Dalam matematika, polinomial atau suku banyak adalah pernyataan matematika yang melibatkan jumlahan perkalian pangkat dalam satu atau lebih variabel dengan koefisien. Sebuah polinomial dalam satu variabel dengan koefisien konstan memiliki bentuk seperti berikut:
Pangkat tertinggi pada suatu polinomial menunjukkan orde atau derajat dari polinomial tersebut.

INTEGRAL TRIGONOMETRI
Integral fungsi trigonometri yaitu kebalikan dari turunan trigonometri. Di mana, integral tersebut juga memuat fungsi trigonometri.

BARISAN DAN DERET
Dalam matematika, barisan[1] (atau banjar[2], atau bahkan secara istilah terkelirukan dengan deret) secara sederhana dapat dibayangkan sebagai suatu daftar benda (seperti bilangan, fungsi, peubah acak, dsb) yang diatur dalam suatu urutan tertentu[3]. Tiap-tiap benda dalam barisan diberi nomor urut atau indeks untuk menunjukkan tempatnya benda tersebut dalam barisan itu[4]. Benda dengan indeks i disebut suku ke-i. Banyak suku dalam barisan (mungkin tak terhingga) disebut panjang barisan.
Deret (bahasa Inggris: series) adalah jumlah suku-suku dari suatu barisan. Barisan dan deret hingga mempunyai elemen pertama dan terakhir yang terdefinisi, sedangkan barisan dan deret tak terhingga berlangsung terus menerus tak terbatas.[1]
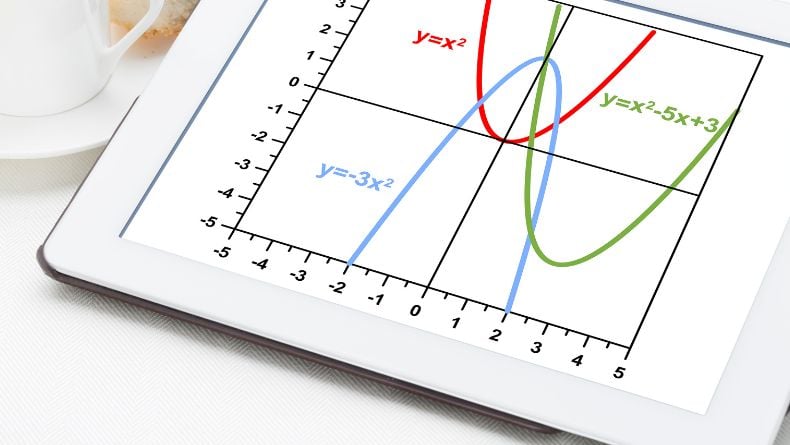
LIMIT FUNGSI ALJABAR
Limit fungsi aljabar adalah batas yang memakai konsep pendekatan fungsi. Suatu fungsi dikatakan tidak terdefinisi pada titik-titik tertentu. Limit bisa dikatakan sebagai nilai yang menuju batas tertentu. Adapun batas tersebut bisa dinilai dekat, namun tidak bisa dicapai.
Konsep Limit Fungsi Aljabar
Setelah mengetahui pengertian dari limit fungsi aljabar, kamu juga perlu memahami konsepnya. Limit fungsi terdiri atas f(x) dan batas x yang dimasukkan ke dalam fungsi. Limit fungsi aljabar terdiri dari beberapa komponen, yakni nilai x mendekati satu titik dan nilai x mendekati tak berhingga (∞). Jika ingin mencari limit fungsi aljabar, maka ada beberapa cara yang bisa diterapkan.
Cara mengerjakan limit fungsi aljabar yakni nilai x yang mendekati berhingga dengan pemfaktoran, substitusi, dan dikalikan sekawannya. Jika x dalam limit fungsi aljabar mendekati tak berhingga, maka penyelesainnya yakni dibagi dengan variabel pangkat tertinggi, lalu dikalikan akar sekawannya. Perlu digarisbawahi bahwa hasil perhitungan limit fungsi aljabar tidak diperbolehkan 0/0 karena nilai tersebut tidak akan bisa terdefinisi.
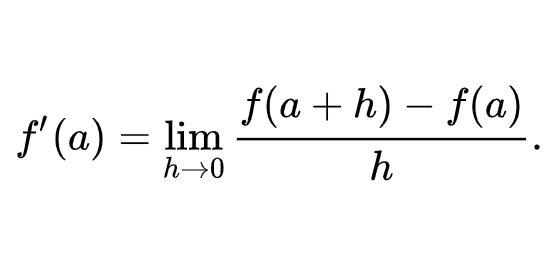
TURUNAN PERTAMA FUNGSI ALJABAR
Turunan atau derivatif dari sebuah fungsi adalah cara mengukur sensitivitas perubahan nilai fungsi terhadap perubahan pada nilai variabelnya. Sebagai contoh, turunan dari posisi sebuah benda bergerak terhadap waktu mengukur kecepatan benda bergerak ketika waktu berjalan. Turunan adalah alat penting dalam kalkulus.
Turunan sebuah fungsi satu variabel di suatu titik, jika itu ada, adalah kemiringan dari garis singgung dari grafik fungsi di titik tersebut. Garis singgung adalah hampiran (aproksimasi) linear terbaik dari fungsi di sekitar titik tersebut. Konsep turunan dapat diperumum untuk fungsi multivariabel. Dalam perumuman ini, turunan dianggap sebagai transformasi linear, dengan translasi yang sesuai, menghasilkan hampiran linear dari grafik fungsi multivariabel tersebut. Matriks Jacobi adalah matriks yang merepresentasikan transformasi linear terhadap suatu basis yang ditentukan. Matriks ini dapat ditentukan dengan turunan parsial dari variabel-variabel independen. Pada fungsi multivariabel bernilai real, matriks Jacobi tereduksi menjadi vektor gradien.
Proses menemukan turunan disebut diferensiasi. Kebalikan proses ini disebut dengan antiturunan. Teorema fundamental kalkulus menyatakan hubungan diferensiasi dengan integrasi. Turunan dan integral adalah dua operasi dasar dalam kalkulus satu-variabel.
Konsep turunan fungsi yang universal banyak digunakan dalam berbagai cabang matematika maupun bidang ilmu yang lain. Dalam bidang ekonomi, turunan digunakan untuk menghitung biaya marginal, total penerimaan, dan biaya produksi. Bidang biologi menggunakan turunan untuk menghitung laju pertumbuhan mikroorganisme, dalam bidang fisika untuk menghitung kepadatan kawat, dalam bidang kimia untuk menghitung laju pemisahan, dalam bidang geografi untuk menghitung laju pertumbuhan penduduk, dan masih banyak lagi.

Grafik fungsi (warna hitam) dan garis tangen pada fungsi (warna merah). Kemiringan dari garis tangen sama dengan turunan fungsi pada titik tersebut.

Kemiringan dari fungsi linear y = f(x) = mx + b adalah

APLIKASI TURUNAN PERTAMA FUNGSI ALJABAR
Turunan fungsi aljabar adalah fungsi baru hasil penurunan pangkat dari fungsi sebelumnya menurut aturan yang telah ditetapkan.
Jika diimplementasikan di dalam grafik fungsi, turunan ini merupakan gradien garis singgung terhadap grafik di titik tertentu.

Kemiringan dari garis tangen /garis singgung sama dengan turunan fungsi pada titik tersebut.

INTEGRAL FUNGSI ALJABAR
Integral merupakan bentuk operasi matematika yang menjadi kebalikan (invers) dari operasi turunan dan limit dari jumlah atau suatu luas daerah tertentu. Berdasarkan pengertian tersebut ada dua hal yang dilakukan dalam integral sehingga dikategorikan menjadi 2 jenis integral. Pertama, integral sebagai invers/ kebalikan dari turunan disebut sebagai Integral Tak Tentu. Kedua, integral sebagai limit dari jumlah atau suatu luas daerah tertentu disebut integral tentu.


LIMIT TRIGONOMETRI
Limit fungsi diartikan sebagai pergerakan nilai fungsi mendekati batasan nilai tertentu yang paling mendekati nilai tersebut namun tidak pernah mencapai nilai tertentu tersebut secara tepat. Penulisan limit fungsi secara umum menggunakan notasi berikut:

Untuk membuktikan limit fungsi trigonometri maka digunakan Teorema Apit. Misal terdapat fungsi h, i, j yang terdefinisi pada interval terbuka L yang memuat a kecuali di a itu sendiri, sehingga berlaku fungsi h(x) ≤ i(x) ≤ j(x) untuk setiap x ϵ L dan x a.

Sehingga berdasarkan Teorema Apit di atas terbukti bahwa nilai limit fungsi trigonometri berikut ini:

Sehingga disimpulkan teorema limit fungsi trigonometri untuk sembarang nilai real a, diperoleh: